1599. Dynamic frog

With the increased use of pesticides, the local streams and rivers have become so contaminated that it has become almost impossible for the aquatic animals to survive.

Frog Fred is on the left bank of such a river. n rocks are arranged in a straight line from the left bank to the right bank. The distance between the left and the right bank is d meters. There are rocks of two sizes. The bigger ones can withstand any weight but the smaller ones start to drown as soon as any mass is placed on it. Fred has to go to the right bank where he has to collect a gift and return to the left bank where his home is situated.

He can land on every small rock at most one time, but can use the bigger ones as many times as he likes. He can never touch the polluted water as it is extremely contaminated.

Can you plan the itinerary so that the maximum distance of a single leap is minimized?

Input. The first line is the number of test cases t (t < 100). Each case starts with a line containing two integers n (0 ≤ n ≤ 100) and d (1 ≤ d ≤ 10⁹). The next line gives the description of the n stones. Each stone is defined by s-m. s indicates the type Big (B) or Small (S) and m (0 < m < d) determines the distance of that stone from the left bank. The stones will be given in increasing order of m.

Output. For each test case print the case number followed by the minimized maximum leap.

Sample input 1	Sample output 1
3 1 10 B-5 1 10 S-5 2 10 B-3 S-6	Case 1: 5 Case 2: 10 Case 3: 7
Sample input 2	Sample output 2
1 6 50 S-2 B-14 S-20 S-26 B-38 S-43	Case 1: 18

SOLUTION

greedy

Algorithm analysis

Obviously, on the way back, the frog can use all the stones on its way. We need to develop a strategy for moving the frog from the left bank to the right. We’ll assume that the left and right banks are large stones, and initially the frog is on the leftmost stone. Now we will replace each large stone with two small ones located in the same place. This can be done since it is obvious that the frog will use any large stone no more than twice. Since now we have a sequence of only small stones, we will formulate an algorithm for the frog’s movement: when moving from the left to the right bank, it must jump over one stone every time – this is the principle of the greedy approach.

Example

Cnsider the second test case. The crossing contains n = 6 stones, the distance between the banks is d = 50. The left and right banks are represented by large stones. The array and the movement of the frog along it is as follows.

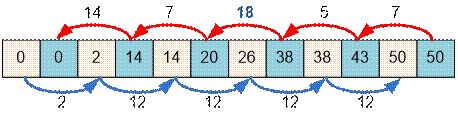
Algorithm realization

Read the input data.

scanf("%d\n",&tests);

for(t = 1; t <= tests; t++)

{

scanf("%d %d\n",&n,&d);

memset(m,-1,sizeof(m));

The left bank is one large stone. Replace it with two small ones.

m[0] = m[1] = 0;

Read the information about stones and store in the m array. Put each large stone into the array twice, each small stone put only once.

for(ptr = 2, i = 0; i < n; i++)

{

do {scanf("%c",&letter);} while (letter == ' ');

scanf("-%d",&s);

if (letter == 'B') {m[ptr] = m[ptr+1] = s; ptr += 2;}

else {m[ptr] = s; ptr++;}

}

Represent the right bank with one large stone. Replace it with two small ones.

m[ptr] = m[ptr+1] = d;

ptr++;

scanf("\n");

Move from the leftmost stone to the rightmost one, jumping over one. We are looking for the maximum differences between the i-th and the (i + 2)-nd stones.

for(dist = 0, i = 2; i < ptr; i += 2)

if (m[i] - m[i-2] > dist) dist = m[i] - m[i-2];

Decrease the value of i by 1. Now we move from right to left along neighboring stones that have odd numbers (stones with even numbers drowned when the frog moved to the right bank).

for(i--; i >= 2; i -= 2)

if (m[i] - m[i-2] > dist) dist = m[i] - m[i-2];

Print the answer.

printf("Case %d: %d\n",t,dist);

}